1、因此,得到y与x的分段函数表达式 2分析第二问可知,该问题就是求最大值问题即 Q=xy=05x#x00B2+50x 求Q对x的一阶导数,令dQdx=0时,得到极值点x所以x对应的Q=1250元 求Q对x的二阶导数,得d#x00B2Qdx#x00B2lt0,所以Q=1250元是最大值 求解过程解 1从图中,可以得到当x=20kg时y=4。
2、ldquo胡不归rdquo问题是初中数学几何中的一类最值问题,主要解决的是rdquoPA+k·PBrdquo型的最值,其中k为任意非1正数,且点P在直线上运动解答要点如下问题背景ldquo胡不归rdquo问题源于古代的一个数学故事,实质上是求解rdquoPA+k·PBrdquo的最小值问题当k=1时,问题转。
3、核心思路应用几何中的不等量性质定理,如两点之间线段最短点到直线垂线段最短等应用场景直接利用几何定理求解最值问题,通常涉及线段长度角度大小等数形结合法 核心思路分析问题变动元素的代数关系,构造二次函数等数学模型,通过图形和代数求解的方式相结合来求解最值应用场景适用于涉及。
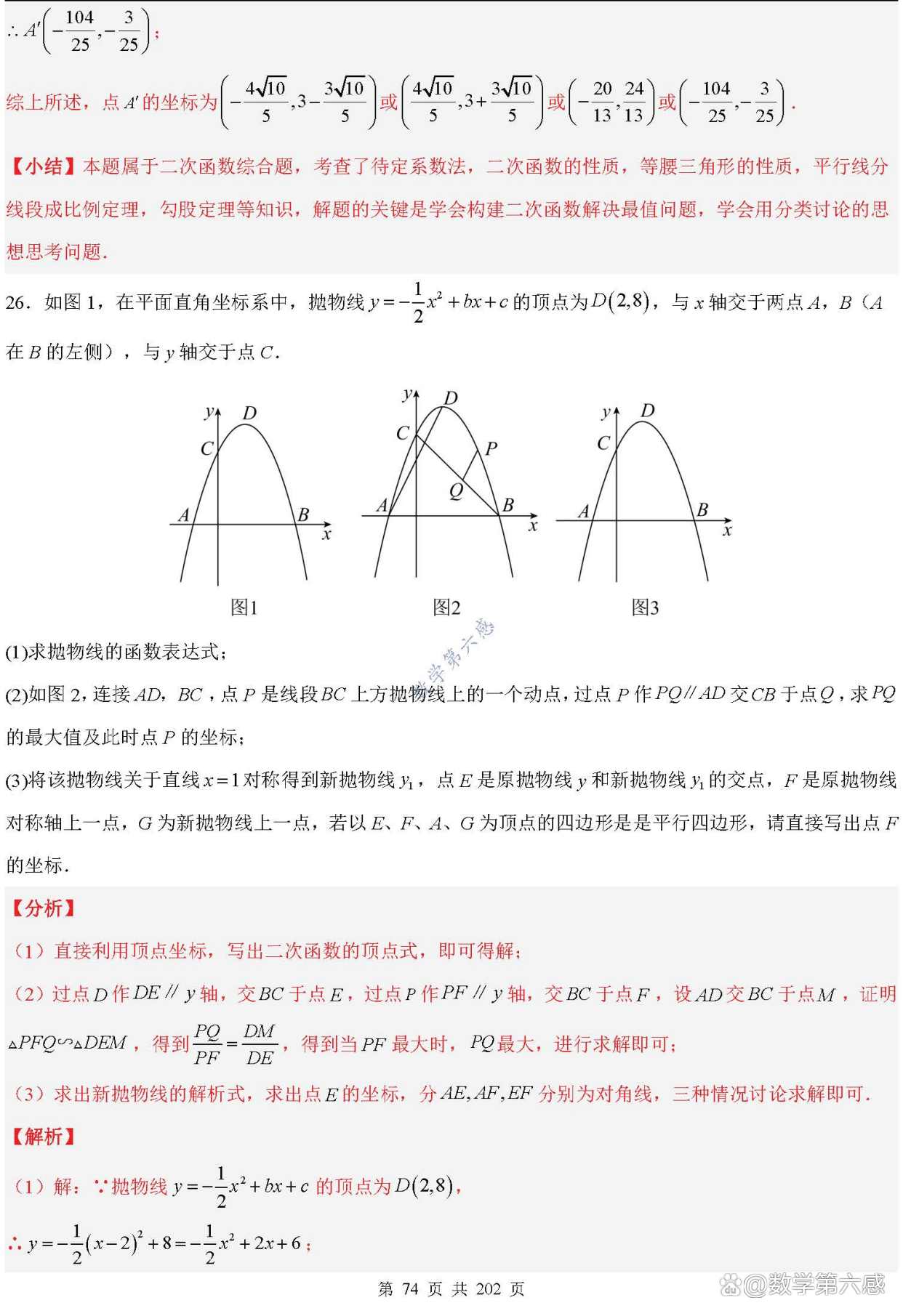
4、初中数学三角形最值问题十大考点总结1 三角形两边之和大于第三边,两边之差小于第三边 考点解析这是三角形的基本性质,也是解决三角形最值问题的基础在给定两边长度时,可以据此确定第三边的取值范围,进而求解最值问题示例若三角形两边分别为3和5,求第三边的取值范围及可能的最值2。
5、由此得出,EF+BF的最小值为3倍根号3,即3×3#189这种解题方法巧妙地利用了对称性和直角三角形的性质,简化了复杂问题,使得求解过程更加直观通过这种方法,我们能够有效地解决几何中最值问题,不仅能够找到最短路径,还能加深对几何图形性质的理解在实际应用中,这样的方法不仅适用于几何最值问题。
6、初中数学想要拿高分必须掌握的动点最值问题解答要点 动点最值问题是初中数学中的一个重要且具有一定难度的知识点,它通常涉及几何代数等多个数学领域的综合运用为了在数学考试中取得高分,掌握动点最值问题的解题方法是至关重要的以下是对动点最值问题的详细解析和解题要点一动点最值问题的基本。
7、当$AF + FH$取得最小值时,点$M$的运动时间最少利用抛物线的性质和几何关系求出$F$的坐标四总结 胡不归问题的关键在于通过构造辅助线,将原问题转化为求两条线段和的最小值问题在解题过程中,需要灵活运用几何性质和三角函数知识,以及勾股定理等数学工具通过不断练习和总结,可以逐渐掌握。
8、最后找到所求点这类问题不仅考察了学生对几何图形的理解和分析能力,还锻炼了学生的逻辑思维和解题技巧此外,这类问题还可以进一步拓展到三维空间中的动点求最值问题,或者结合其他数学知识如函数方程等进行更复杂的求解但无论如何,掌握基本的解题方法和思路是解决这类问题的关键。
9、在初中数学中,动点求定点距离最值问题是一类常见且具有一定难度的几何问题这类问题通常涉及到一个或多个动点在特定条件下移动,并需要找到某个定点到动点的距离达到最值最大值或最小值时的位置以下是对这类问题的详细解读一问题背景与核心动点求最值问题往往源于实际生活中的优化需求,如“。
10、用配方法求最值问题 在初三数学中,配方法是一种重要的代数技巧,它不仅可以帮助我们解二次方程,还可以用来求解二次函数的最值问题最值问题在数学和实际应用中都非常常见,比如求利润最大化成本最小化等一配方法的基本原理 配方法的核心思想是将一个二次多项式转化为完全平方的形式对于一般。
11、3 初中数学经典最值问题之阿氏圆问题阿氏圆问题与胡不归问题相似,通常通过构造子母相似三角形来转换线段,以解决最值问题4 初中数学经典最值问题之“一箭穿心”模型在解决最值问题时,“一箭穿心”模型常与其他模型如定弦定圆的隐圆模型将军饮马模型等结合使用5 配方法当函数表达式中。
12、取A y轴的对称点M,取B x轴的对称点N,连接MN交Y轴于D#39,交X轴于C#39,则四边形ABC#39D#39为所求如图。
13、这是一个非常古老的数学问题,曾经是历史上非常著名的“难题”,典型特质是求AP+k·BP的形式“PA+k·PB”型的最值问题是中考考查的热点,此类问题的处理通常以动点P所在图像的不同来分类,其中点P在直线上运动的类型称之为“胡不归”问题,而点P在圆周上运动的类型称之为“阿氏圆”问题。
14、如“将军饮马”“造桥选址”等经典模型,通常涉及线段和的最小问题解决这类问题时,可构造对称点或利用圆的性质进行转化,从而找到最小路径对于最大值问题,直径往往具有关键作用,可通过构造直径或利用直径的性质进行求解综上所述,初中数学中证明线段不等关系或最值问题的常用思想方法原理与技巧主要包括利用最基本原理。
15、涉及的数学思想方法也很多,其中函数思想模型思想化归思想尤为突出,因此备受命题者的青睐 学生不仅需要夯实与求最值有关的知识并熟练基本模型的建构,善于从复杂的陌生的图形中分离或构造出基本模型,还要对解题思路和模型选择的方法多反思多总结,只有这样,才能灵活应对几何最值问题。
16、动点最值问题在数学压轴题中常见,解决这类问题的模型和方法多种多样,下面列举了19种常见模型,以帮助理解与解题1将军饮马模型对称点模型利用对称性简化问题2利用三角形两边差求最值通过求解三角形两边之差的最大或最小值解决问题3手拉手全等取最值利用全等三角形的性质,找出最。
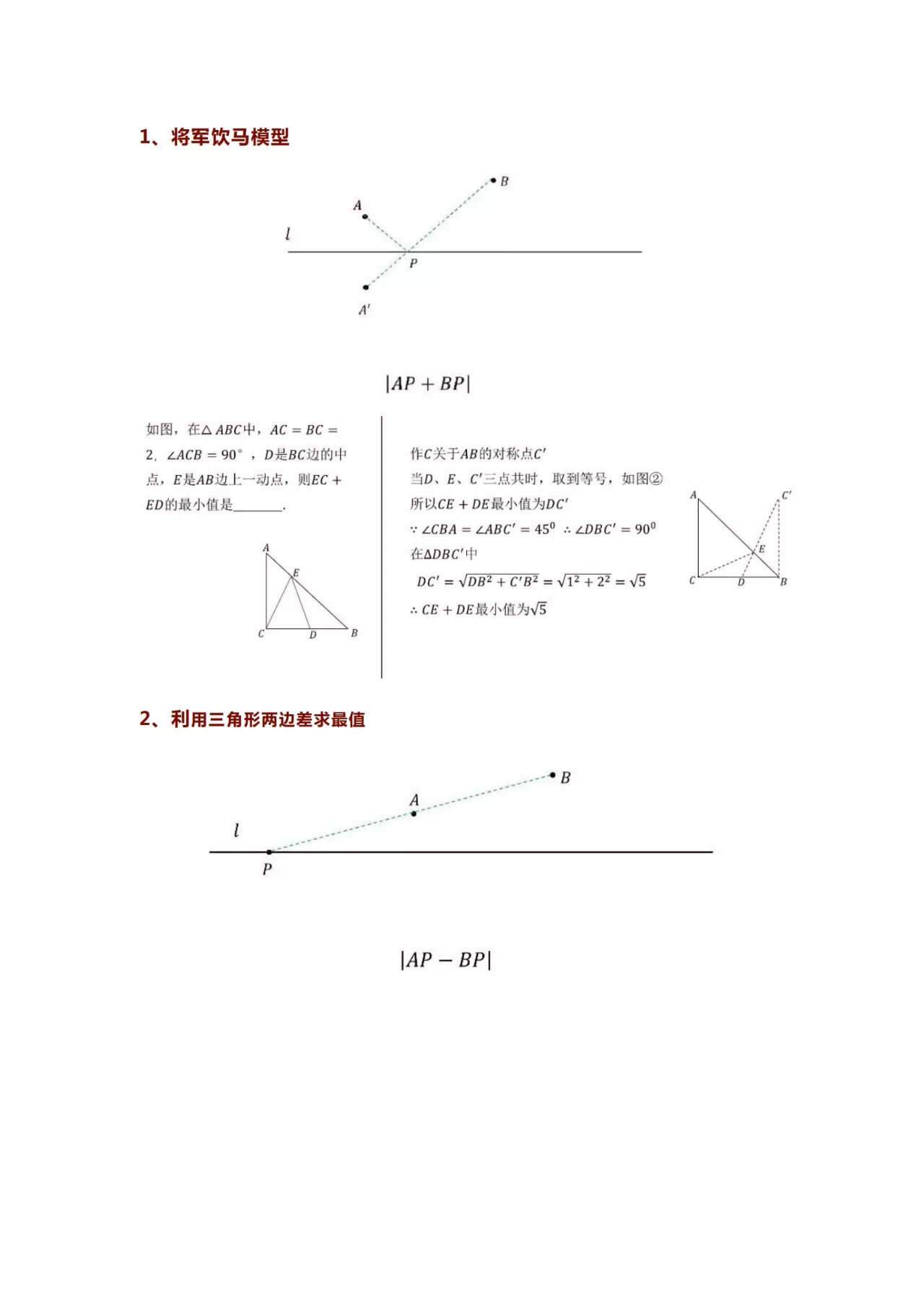


发表评论